Extracción de características estructurales de una imagen ( II ) (Semi-variograma de una imagen usando R).

Nota: Este es un viejo post que he recuperado del blog de GIS&Chips. No sé si ya existe, pero probablemente sería interesante disponer de una librería para realizar este tipo de análisis GEOBIA.

En este artículo usaremos una librería de R (“fields”), que contiene métodos para calcular el semi-variograma empírico de una imagen, lo cual quiere decir que calcularemos el semi-variograma de una gran cantidad de puntos. Y a partir de ahí, analizaremos la existencia de patrones espaciales en tres parcelas agrícolas arbóreas.

Espero que este sea el primero de varios posts donde aprendamos a estudiar las ortoimagenes, extrayendo características de distintos tipos como ya hicimos en un post anterior. En aquel caso, se extrajeron algunas sencillas frecuencias a partir del cálculo de la Transformada de Hough que nos proporcionaba AForge.NET, lo cual nos servía para automatizar la decisión de si una parcela era una plantación arbórea y realizar un conteo automático del número de árboles que contenía. En dicho post, se ofrece una aplicación llamada RAPID, que incorpora una galería de imágenes de parcelas agrícolas. Hemos extraído tres de ellas para realizar los siguientes análisis. Son las siguientes:

Al estudiar las 3 parcelas que aparecen en la primera imágen con el RAPID: La primera es identificada totalmente como agrícola y nos permite contar con bastante certidumbre el número de árboles de un modo automático. En el caso de la segunda, su estructura en hileras no permite el conteo de árboles pues están muy juntos. Y por último, en los olivos de la tercera no se cumplía la regla de una estructura normal, aunque sí que podíamos contar los árboles. Este último caso era el único donde RAPID no podía “acertar” pues identificaba la parcela como no agrícola debido a que la diferencia angular entre las direcciones principales de la Transformada de Hough no se aproximaba a 90º.

¿Qué es un variograma experimental? (una breve explicación para entender los resultados).

Los variogramas se utilizan para caracterizar la posible estructura espacial de un conjunto de datos. Podemos distinguir dos tipos de variogramas, el experimental y el modelizado. De estos nos interesa más el experimental. Este último se usa para describir los datos de una muestra, habitualmente una nube de puntos (xyz)

Matemáticamente el semi-variograma, o variograma/2, se puede definir como la mitad del promedio de las diferencias al cuadrado.

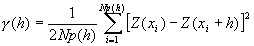
Donde Np(h) es el número de pares a la distancia h, h es el incremento.

Z(xi) son los valores experimentales.

xi localizaciones donde son medidos los valores z(xi).

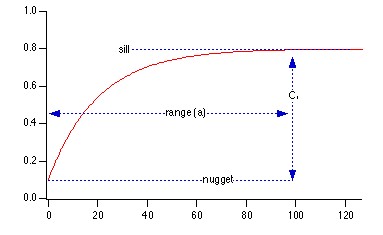
Aplicado a imágenes, el semi-variograma (o variograma/2), mide el grado de correlación espacial entre los píxeles de una imagen. Podemos comentar varios conceptos (ver Figura 3):

• Sill o meseta: representa la varianza máxima.
• Range, rango o alcance: muestra la distancia (en nuestro caso en píxeles) a la que el semi-variograma alcanza la meseta.
• Nugget o “efecto pepita”, es la discontinuidad en el origen. Ésta es debida a que el semivariograma, en la práctica, no es nulo en el origen.

Ejemplos de cálculo en R

Os aviso de que las imágenes referidas en el código estan en formato *.ppm aunque R tiene muchas librerías capaces de convertir a este formato. También podéis utilizar OpenOffice.

En este post, aplicamos el siguiente código para calcular el semi-variograma empírico de cada una de estas imágenes:

# Instalo los packages necesarios:
install.packages("pixmap", dependencies= T)
install.packages("fields", dependencies= T)

# Cargo las librerias:
library(pixmap)
library(fields)

# Hago una lista con las imagenes de las parcelas y las cargo todas:
imag_dir <- list.files("C:\\ ... \\Articulos Gisandchips\\ parcelas_ppm\\", full.names=T)

parcela1 <- read.pnm(imag_dir[1])
parcela2 <- read.pnm(imag_dir[2])
parcela3 <- read.pnm(imag_dir[3])

# Aislamos una banda...
matriz1<-parcela1@green
matriz2<-parcela2@green
matriz3<-parcela3@green

# Calculamos el semivariograma (si queremos podemos acabar antes cambiando el alcance de 40  a 10, por ejemplo, pero los resultados pueden cambiar y quedará menos bonito
vgram1_40<-vgram.matrix( matriz1, R=40) # esto llevará un poco de tiempo
vgram2_40<-vgram.matrix( matriz2, R=40) # esto llevará un poco de tiempo
vgram3_40<-vgram.matrix( matriz3, R=40) # esto llevará un poco de tiempo

# Añadimos al Plot las matrices que acabamos de calcular
plot.vgram.matrix(vgram1_40) # La matriz del variograma
plot.vgram.matrix(vgram2_40) # La matriz del variograma
plot.vgram.matrix(vgram3_40) # La matriz del variograma

# Creamos una curva que ajuste bien sobre la muestra y la añadimos al variograma
polyfit1_40_20 <- lm(vgram1_40$vgram ~ poly(vgram1_40$d, 20));
plot(vgram1_40$d, vgram1_40$vgram)
lines(sort(vgram1_40$d), polyfit1_40_20$fit[order(vgram1_40$d)], col=2, lwd=4)

polyfit2_40_20 <- lm(vgram2_40$vgram ~ poly(vgram2_40$d, 20));
plot(vgram2_40$d, vgram2_40$vgram)
lines(sort(vgram2_40$d), polyfit2_40_20$fit[order(vgram2_40$d)], col=2, lwd=4)

polyfit3_40_20 <- lm(vgram3_40$vgram ~ poly(vgram3_40$d, 20));
plot(vgram3_40$d, vgram3_40$vgram)
lines(sort(vgram3_40$d), polyfit3_40_20$fit[order(vgram3_40$d)], col=2, lwd=4)

El plot que obtenemos es el siguiente, o similar si es que hemos preferido cambiar algún parámetro:

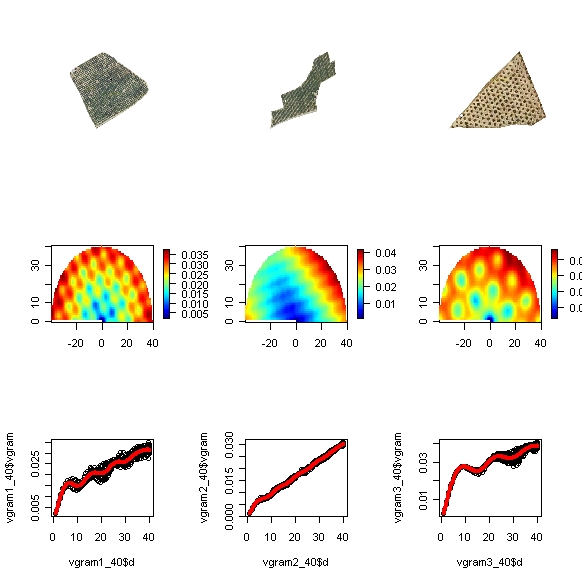
En la imagen vemos las parcelas, la matriz de su variograma y el variograma, con una curva que ajustamos mucho al los datos. Es fácil interpretar que en la estructura de las parcelas se llega a apreciar cierta ciclicidad, ya que encontramos mesetas a distintas distancias. Cada meseta se  corresponde aproximadamente a las hileras de árboles. El alcance es el que hemos definido (40, en este caso 40 píxeles; puede que unos 20 m. en la realidad).

Viendo estas imágenes nos podemos dar cuenta de que es más fácil determinar una regla de clasificación que cuando lo hacíamos en el caso del RAPID. En este caso, nos fijamos en el número de máximos relativos de la función polinómica de ajuste del variograma. A simple vista, la primera parcela tiene unos 4, la segunda apenas 1 y la última 3 o 4. En este caso, podríamos citar una nueva regla para nuestro programa según la que a partir de 2 o 3 máximos relativos una parcela puede ser considerada una plantación arbórea.

Como nos interesa automatizar la tarea creamos una función que nos cuente los máximos relativos. Aquí viene el ejemplo aplicado a la primera parcela:

# Encontrar máximos relativos en la función 1
maxRelativos1=0
hMaxRelativos1=0

for(i in 1:(length(polyfit1_40_20$fitted.values)-1))
{

if (polyfit1_40_20$fitted.values[i] > polyfit1_40_20$fitted.values[i+1] && polyfit1_40_20$fitted.values[i] > polyfit1_40_20$fitted.values[i-1])

{
maxRelativos1[i]<- polyfit1_40_20$fitted.values[i]
hMaxRelativos1[i]<- vgram1_40$d[i]}
}

MaxRelativos1<-data.frame(hMaxRelativos1,maxRelativos1)
MaxRelativos1<- na.omit(MaxRelativos1)
NumMaxRelat1_40<-length(rownames(MaxRelativos1))

Consultamos los vértices de la curva que hemos dibujado mediante un bucle, de modo que si el vértice i tiene un valor superior al vértice anterior y también al vértice posterior entonces es considerado un máximo relativo y queda almacenado en la lista.

Algunos comentarios sobre todo esto:

1. El semivariograma implica un gran esfuerzo de cálculo por parte del ordenador. Esto hace que aún habiendo varias librerías en R que obtienen el semivariograma de una nube de puntos, sean significativamente más lentas que Fields. Además, Fields hace directamente lo que necesitábamos. No obstante, en un futuro no muy lejano, intentaré desarrollar una librería en C# para reproducir un análisis de este tipo y otras cosillas relacionadas.

2. Por cuestiones de tiempo no he tratado de crear funciones para las distintas etapas de la demostración. Puede ser un buen ejercicio tratar de implementar todo esto en funciones que permitan entre sus parámetros especificar la banda con la que trabajar, el alcance del semivariograma…

3. Existen más posibilidades a la hora de establecer reglas, por ejemplo podríamos explorar la distancia que separa los máximos relativos para distinguir los cultivos más intensivos de los más tradicionales. Se me ocurren muchas más posibilidades.

4. Por último, aunque no le doy mucha importancia, deciros que el número de máximos relativos no es del todo correcto pues el cero siempre aparece en el conteo (sale 5, 2, 5 y no 4, 1, 4 como he dicho más arriba), esto es porqué no he trabajado bastante el bucle, pero es fácil restar 1 a la lista final.  Mi idea principal es la de explorar el concepto y dar unos ejemplos de código a modo de ideas.

Referencias:

Para entender bien todo esto creo que es interesante ver el artículo anterior.

Solamente os remito al siguiente tutorial de Surfer. Es bastante didáctico. http://www.goldensoftware.com/variogramTutorial.pdf

De todos modos la red está llena de materiales, apuntes de clase, libros en PDF… No tendréis problemas en encontrar información sobre los variogramas.