Crear teselaciones (repitiendo formas hasta decir ¡basta!)
Nota: Este es un no tan viejo post de GIS&Chips en el que presentaba una aplicación de consola para generar teselaciones regulares utilizando NTS. El post sigue siendo el mismo pero ahora podéis descargar el proyecto de VisualStudio que he compartido en GitHub [Ir al proyecto].
Según la Wikipedia, un teselado o teselación es una regularidad o patrón de figuras que cubre completamente una superficie, sin dejar huecos y sin que las figuras se superpongan. Los que habéis trabajado mucho con SIG ya tenéis una buena idea de a que me estoy refiriendo.
En este post quiero hablaros un poco más de las teselaciones, comentar algunas aplicaciones y proponeros algo de código de ejemplo. Utilizando software libre, por supuesto…

Además, en la wikipedia se puede ver que existen numerosos tipos de teselaciones. De un modo general, éstas se pueden clasificar en teselaciones regulares, semirregulares e irregulares. Generalmente, en SIG se suelen utilizar distintas teselaciones regulares e irregulares para el análisis de zonas geográficas. Las teselaciones irregulares (Voronoi y Delaunay, de todo tipo) dan mucho juego. Podemos encontrar libros y publicaciones científicas de lo más interesantes (por ejemplo, podrías dedicar meses a leer y releer el libro Spatial Tessellations. Sin embargo, en este post nos centraremos en las teselaciones regulares más simples y las variaciones que pueden experimentar (ver la figura de arriba).
¿Para qué sirven?
Las aplicaciones de las teselaciones en Geografía y SIG son muchas. Por mencionar algunas de las más habituales:
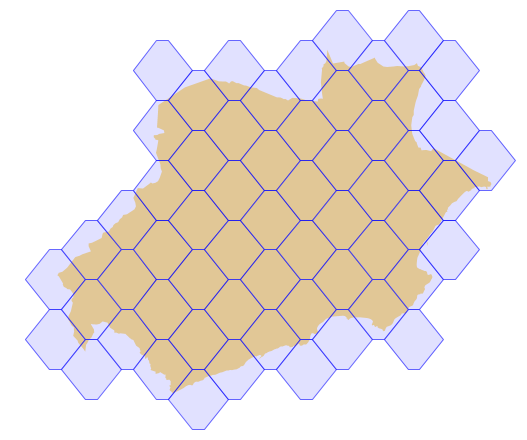
- Estudios del paisaje a distintas escalas. En las siguiente figura podéis apreciar lo que sucedería si calculásemos el valor medio de los píxeles dentro de cada hexágono. Si tratásemos de contar las “celdas” que están mayormente ocupadas por el amarillo más intenso, obtendríamos valores distintos. Este tipo de consideraciones son muy tenidas en cuenta en los estudios de Ecología del Paisaje. Es necesario seleccionar la forma del grid, sus dimensiones y también su orientación. Esto nos dará una idea de la estructura espacial del paisaje. En la bibliografía se habla de “escalogramas” para estudiar los efectos del grid (Wu et al., 2002)
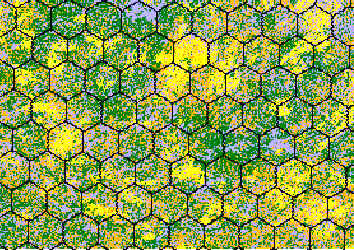

http://www.cnfer.on.ca/SEP/patchanalyst/overview.htm
- Muestreos de la zona de estudio. Son muy utilizados en estudios biogeográficos donde se determina la presencia-ausencia de una determinada especie. Por ejemplo, el código que presento en este post fue desarrollado para un estudio de fototrampeo .
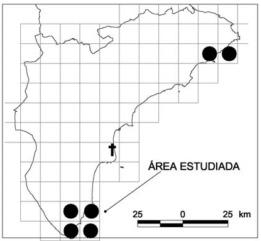
- Diseño de cartografía. El ejemplo más típico de uso de una cuadrícula es el del mapa turístico donde se utiliza un grid para localizar de manera relativa los elementos de interés. También se suelen crear cuadrículas UTM o se crean Mapbooks que organizan una serie de mapas.


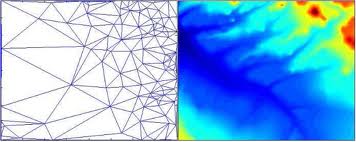
- Interpolación espacial. En este caso predomina el uso de teselaciones no regulares. Por ejemplo, las triangulaciones de Delaunay son una alternativa muy utilizada para la creación de modelos digitales de elevaciones detallados. Igualmente, los polígonos de Voronoi se han utilizado en múltiples contextos, por ejemplo, para determinar la necesidad de instalar nuevos observatorios meteorológicos.
Software de ejemplo
Si tuviese que mencionar un software interesante para realizar teselaciones os recomendaría echarle un vistazo al Repeating Shapes for ArcGIS. Se trata de una extensión de ArcGIS, creada por el biólogo Jeff Jenness, que permite crear las teselaciones básicas, modificándolas según distintos parámetros (forma, dimensiones y ángulos). El manual que aparece en la web resulta muy explicativo para entender las teselaciones más básicas. Sin embargo, esta extensión es muy limitada si tenemos la necesidad de generar muchos grids, o añadir nuevos parámetros. Además, como hemos dejado entrever, existen muchas otras configuraciones posibles que este software no contempla.
Propuesta de software
He decidido ordenar un poco mis ideas y he creado un software que calcula teselaciones simples (rectángulos, triángulos y hexágonos). Se trata de una aplicación de consola que solicita una serie de parámetros para calcular la teselación. Esta aplicación utiliza la NetTopologySuite v1.11 y funciona bien sobre la versión 4.0 de la plataforma Mono.
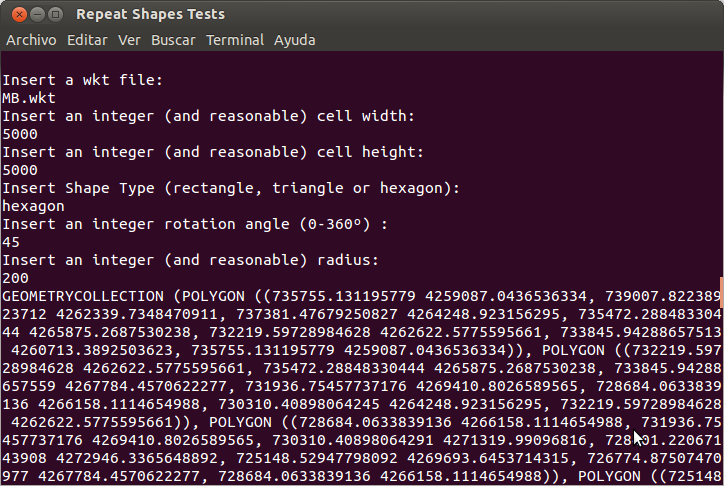
Como podéis ver los parámetros son los siguientes:
- un fichero que contenga una geometría en formato “Well-Known Text” (se pide un fichero ya que una geometría completa nos ocuparía toda la pantalla).
- el alto y ancho de cada “celda”.
- el tipo de forma deseada (rectángulo, triángulo o hexágono).
- el ángulo de rotación de la teselación y, en caso de tratarse de hexágonos,
- un radio, que es una medida que define el estiramiento de los polígonos (no creo que sea la manera habitual de crear estas geometrías, pero da mucha flexibilidad).
Finalmente, el programa calcula la teselación y pregunta si quereis crear otra teselación más (no creo que resulte adictivo :-) El resultado que genera el software es una WKT GeometryCollection, que podemos visualizar en distintos SIG de escritorio (yo utilizo OpenJump).
Una vez definidos los parámetros de entrada, hay algunas cuestiones que pueden resultar interesantes sobre el programa.
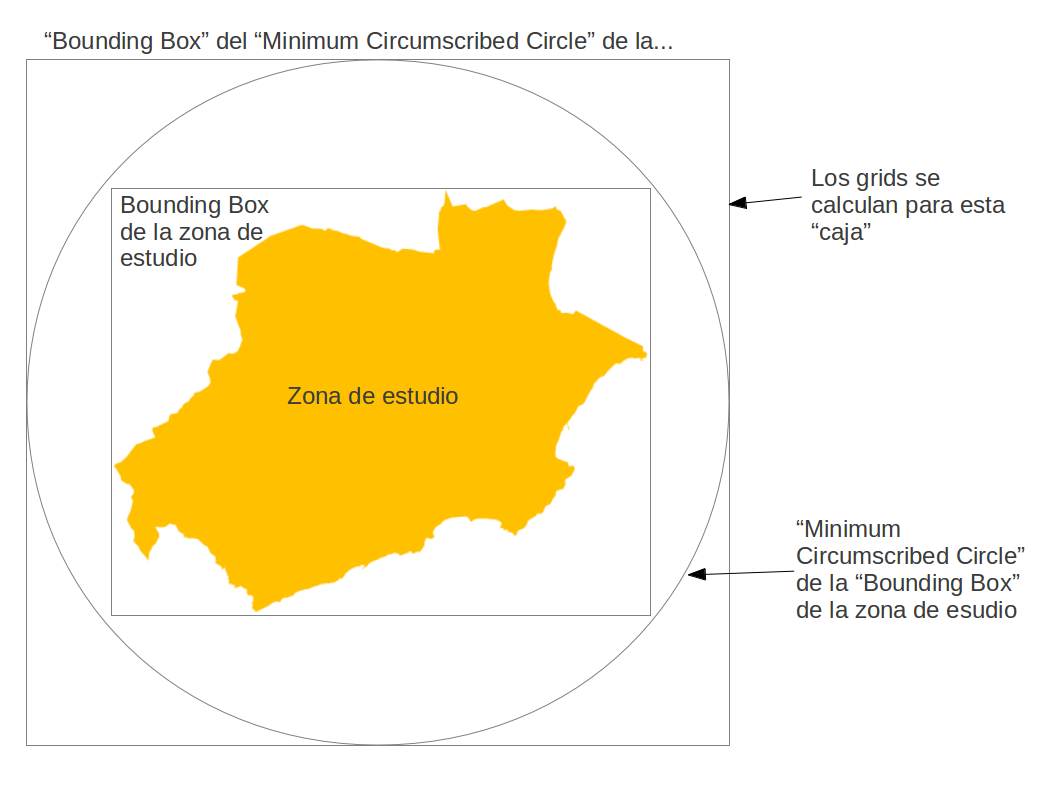
El código se divide en dos clases (más la del interfaz de usuario, claro). Existe una clase (1) MyGeometricShapeFactory que calcula triángulos y hexágonos a partir de los parámetros de entrada. Esta clase hereda de la GeometricShapeFactory de NTS, que se ocupa de crear los rectángulos. Por otro lado, existe otra clase (GraticuleBuilder; 2) que se ocupa de la repetición de figuras (haciendo servir la clase 1). Esta clase (2) permite crear un grid mucho mayor que la zona de estudio y filtrarlo con operadores espaciales para obtener otro “grid ajustado” a la zona de estudio.
En la siguiente figura se puede ver como se calcula la zona que debe cubrir el grid mayor. Por supuesto, habrá otros métodos de definir el área mayor, pero esta es bastante sencilla de entender y programar con NTS.
Algunos ejemplos utilizando esto:
Para que os hagáis una idea de lo que permite el software he preparado algunos ejemplos interesantes:
- Ancho de celda: 5000 m, Alto de celda: 5000 m, Forma: rectangle, Ángulo: 0 y Radio: 0 (Completo).
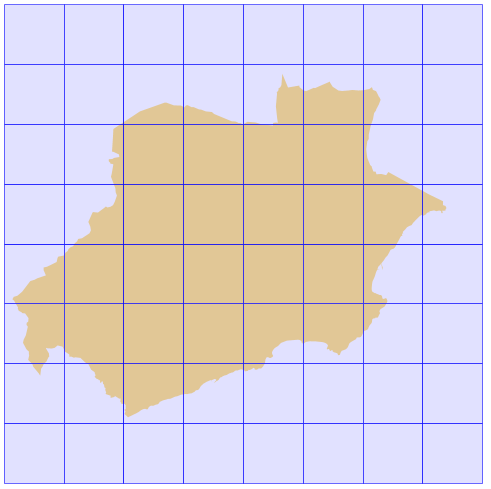
- Ancho de celda: 2500 m, Alto de celda: 2500 m, Forma: rectangle, Ángulo: 0 y Radio: 0 (Ajustado).

- Ancho de celda: 5000 m, Alto de celda: 1000 m, Forma: rectangle, Ángulo: 0 y Radio: 0 (Ajustado).

- Ancho de celda: 5000 m, Alto de celda: 2500 m, Forma: triangle, Ángulo: 45 y Radio: 0 (Ajustado).
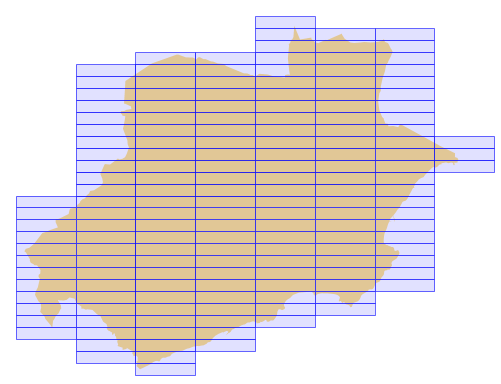
- Ancho de celda: 5000 m, Alto de celda: 5000 m, Forma: hexagon, Ángulo: 45 y Radio: 1000 m (Ajustado).
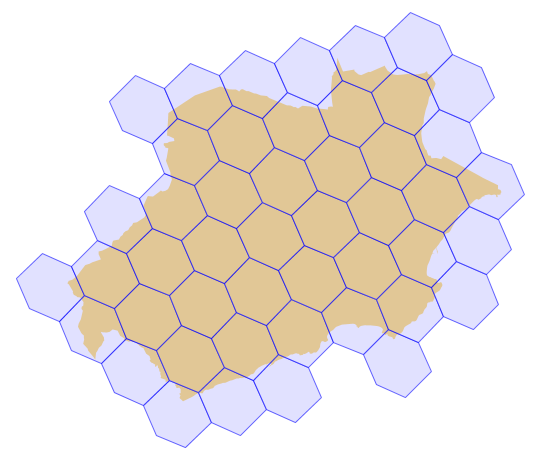
- Ancho de celda: 5000 m, Alto de celda: 5000 m, Forma: hexagon, Ángulo: 0 y Radio: 2000 m (Ajustado).
Código comentado:
A continuación os adjunto el código que hace todo esto posible. No incluyo lo referente al UI, pero comprobareis que tampoco hay que hacer nada del otro mundo para utilizarlo (new GraticuleBuilder). Además, os tendréis que crear un enumerado con las formas (rectangle, triangle y hexagon).
Primero tenéis la clase que crea la tesela:
//GraticuleBuilder class for creating tessellations.
//Copyright (C) 2012 Benito M. Zaragozi
//Authors: Benito M. Zaragozi (www.gisandchips.org)
//Send comments and suggestions to benito.zaragozi@ua.es
//This program is free software: you can redistribute it and/or modify
//it under the terms of the GNU General Public License as published by
//the Free Software Foundation, either version 3 of the License, or
//(at your option) any later version.
//
//This program is distributed in the hope that it will be useful,
//but WITHOUT ANY WARRANTY; without even the implied warranty of
//MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
//GNU General Public License for more details.
//
//You should have received a copy of the GNU General Public License
//along with this program. If not, see <http://www.gnu.org/licenses/>.
using System;
using System.Collections;
using System.Collections.Generic;
using NetTopologySuite.IO;
using NetTopologySuite.Geometries;
using NetTopologySuite.Utilities;
using GeoAPI.Geometries;
namespace RepeatShapes
{
public class GraticuleBuilder
{
public GraticuleBuilder (IGeometry studyArea,int cellWidth, int cellHeight, ShapeType shp, int angle, int radius)
{
_studyArea=studyArea;
GetBigArea (_studyArea,cellWidth,cellHeight);
_origin=GetOrigin (_bigArea);
if(shp== ShapeType.rectangle)
{
_bigGrid = rectRepeat(cellWidth,cellHeight,_bigGridRows,_bigGridCols);
}
else if(shp==ShapeType.triangle)
{
_bigGrid = triRepeat(cellWidth,cellHeight,_bigGridRows,_bigGridCols);
}
else if(shp==ShapeType.hexagon)
{
_bigGrid = hexRepeat(cellWidth,cellHeight,_bigGridRows,_bigGridCols, radius);
}
_bigGrid = rotateGrid (_bigGrid, _studyArea, angle);
_filteredGrid=gridFilter(_bigGrid,_studyArea);
}
IGeometry _studyArea;
IGeometry _bigArea;
IPoint _origin;
GeometryCollection _bigGrid;
GeometryCollection _filteredGrid;
int _bigGridRows=0;
int _bigGridCols=0;
public IGeometry StudyArea {
get { return _studyArea; }
}
public GeometryCollection BigGrid
{
get{return _bigGrid;}
}
public GeometryCollection FilteredGrid
{
get{return _filteredGrid;}
}
/// <summary>
/// Calculates the left-bottom coordinate/point of a geometry.
/// </summary>
/// <returns>
/// The origin point for the grid.
/// </returns>
/// <param name='bigAreaEnvelope'>
/// A big area that encloses the study area.
/// </param>
private Point GetOrigin(IGeometry bigAreaEnvelope)
{
double minX=0;
double minY=0;
foreach(Coordinate c in bigAreaEnvelope.Coordinates)
{
minX = c.X;
minY = c.Y;
if(c.X < minX)
{
minX=c.X;
}
if(c.Y<minY)
{
minY=c.Y;
}
}
Point p = new Point(minX,minY);
return p;
}
/// <summary>
/// Create a big rectangle containing the study area.
/// </summary>
/// <param name="studyArea"></param>
/// <param name="widthDivBy"></param>
/// <param name="heightDivBy"></param>
private void GetBigArea(IGeometry studyArea, int widthDivBy, int heightDivBy)
{
//circumscribed circle for obtaining its envelope and create the bigArea.
NetTopologySuite.Algorithm.MinimumBoundingCircle mbc =
new NetTopologySuite.Algorithm.MinimumBoundingCircle(studyArea);
_bigArea = mbc.GetCircle ().Envelope.Boundary;
double diameter = mbc.GetRadius ()*4;
//get the total num of cols and rows
_bigGridCols=(int)diameter/widthDivBy;
_bigGridRows=(int)diameter/heightDivBy;
}
/// <summary>
/// Rotates the bigGrid.
/// </summary>
/// <returns>
/// The rotated grid.
/// </returns>
/// <param name='bigGrid'>
/// The grid that overlaps the bigArea.
/// </param>
/// <param name='studyArea'>
/// The region of interest.
/// </param>
/// <param name='degree'>
/// A rotation angle in decimal degrees.
/// </param>
private GeometryCollection rotateGrid(GeometryCollection bigGrid, IGeometry studyArea, int degree)
{
NetTopologySuite.Geometries.Utilities.AffineTransformation trans =
NetTopologySuite.Geometries.Utilities.AffineTransformation.RotationInstance(
Degrees.ToRadians (degree),studyArea.Centroid.X, studyArea.Centroid.Y);
return (GeometryCollection)trans.Transform (bigGrid);
}
/// <summary>
/// Filter the bigGrid for achieving a grid adjusted to the region of interest.
/// </summary>
/// <returns>
/// A grid adjusted to the region of interest.
/// </returns>
/// <param name='bigGrid'>
/// A grid that exceeds the region of interest.
/// </param>
/// <param name='studyArea'>
/// The region of interest.
/// </param>
private GeometryCollection gridFilter(GeometryCollection bigGrid, IGeometry studyArea)
{
List<IGeometry>filteredGrid=new List<IGeometry>();
foreach(IPolygon p in bigGrid.Geometries)
{
if(p.Intersects(studyArea)==true)
{
filteredGrid.Add(p);
}
}
return new GeometryCollection(filteredGrid.ToArray ());
}
/// <summary>
/// Creates a rectangular tessellation.
/// </summary>
/// <returns>
/// A rectangular grid.
/// </returns>
/// <param name='cellWidth'>
/// Cell width.
/// </param>
/// <param name='cellHeight'>
/// Cell height.
/// </param>
/// <param name='numRows'>
/// Number of rows.
/// </param>
/// <param name='numColumns'>
/// Number of columns.
/// </param>
private GeometryCollection rectRepeat(int cellWidth, int cellHeight, int numRows, int numColumns)
{
List<IGeometry> bigGrid = new List<IGeometry>();
double x = _origin.X;
double y = _origin.Y;
GeometricShapeFactory gsf = new GeometricShapeFactory();
gsf.Height=Convert.ToDouble(cellHeight);
gsf.Width=Convert.ToDouble(cellWidth);
gsf.NumPoints=4;
for (int i = 1; i <= numColumns; i++)
{
for (int j = 1; j <= numRows; j++)
{
gsf.Base=new Coordinate(x, y);
IPolygon newpol = gsf.CreateRectangle();
newpol.UserData=i+" - "+j;
bigGrid.Add(newpol);
y += cellHeight;
}
if(i!=0)
{
x += cellWidth;
}
y = _origin.Y;
}
return new GeometryCollection(bigGrid.ToArray ());
}
/// <summary>
/// Creates a triangular tessellation.
/// </summary>
/// <returns>
/// A triangular tessellation.
/// </returns>
/// <param name='cellWidth'>
/// Cell width.
/// </param>
/// <param name='cellHeight'>
/// Cell height.
/// </param>
/// <param name='numRows'>
/// Number of rows.
/// </param>
/// <param name='numColumns'>
/// Number of columns.
/// </param>
private GeometryCollection triRepeat(int cellWidth, int cellHeight, int numRows, int numColumns)
{
List<IGeometry> bigGrid = new List<IGeometry>();
double x = _origin.X-cellWidth;
double y = _origin.Y;
MyGeometricShapeFactory gsf = new MyGeometricShapeFactory();
gsf.Height=cellHeight;
gsf.Width=cellWidth;
gsf.NumPoints=4;
for (int i = 1; i <= numColumns*2; i++)
{
for (int j = 1; j <= numRows; j++)
{
if (i % 2 == 0)
{
gsf.Centre=new Coordinate(x, y);
gsf.Envelope=new Envelope(x,x+cellWidth,y,y+cellHeight);
IPolygon newpol = gsf.CreateTriangle();
newpol.UserData=i+" - "+j;
bigGrid.Add(newpol);
}
else
{
gsf.Centre=new Coordinate(x, y);
gsf.Envelope=new Envelope(x+cellWidth/2,x+cellWidth/2+cellWidth,y,y+cellHeight);
IPolygon newpol = gsf.CreateInvertedTriangle();
newpol.UserData=i+" - "+j;
bigGrid.Add(newpol);
}
y += cellHeight;
}
if(i % 2!=0)
{
x += cellWidth;
}
y = _origin.Y;
}
return new GeometryCollection(bigGrid.ToArray ());
}
/// <summary>
/// Creates an hexagonal tessellation.
/// </summary>
/// <returns>
/// The hexagonal tessellation
/// </returns>
/// <param name='cellWidth'>
/// Cell width.
/// </param>
/// <param name='cellHeight'>
/// Cell height.
/// </param>
/// <param name='numRows'>
/// Number of rows.
/// </param>
/// <param name='numColumns'>
/// Number of columns.
/// </param>
/// <param name='radius'>
/// A proportion that defines the longitude of the hexagon's base.
/// A larger radius is relate with a narrower base of the hexagon.
/// </param>
private GeometryCollection hexRepeat(int cellWidth, int cellHeight, int numRows, int numColumns, int radius)
{
List<IGeometry> bigGrid = new List<IGeometry>();
double x = _origin.X-cellWidth;
double y = _origin.Y;
MyGeometricShapeFactory gsf = new MyGeometricShapeFactory();
gsf.Height=cellHeight;
gsf.Width=cellWidth;
gsf.NumPoints=4;
for (int i = 1; i <= numColumns*2; i++)
{
for (int j = 1; j <= numRows; j++)
{
if (i % 2 == 0)
{
gsf.Centre=new Coordinate(x, y);
gsf.Envelope=new Envelope(x,x+cellWidth,y,y+cellHeight);
IPolygon newpol = gsf.CreateHexagon(radius);
newpol.UserData=i+" - "+j;
bigGrid.Add(newpol);
}
else
{
gsf.Centre=new Coordinate(x, y);
gsf.Envelope=new Envelope(x+(cellWidth-radius),x+cellWidth+(cellWidth-radius),y+(cellHeight/2),y+cellHeight+(cellHeight/2));
IPolygon newpol = gsf.CreateHexagon(radius);
newpol.UserData=i+" - "+j;
bigGrid.Add(newpol);
}
y += cellHeight;
}
if(i % 2!=0)
{
x += cellWidth+(cellWidth-2*radius);
}
y = _origin.Y;
}
return new GeometryCollection(bigGrid.ToArray ());
}
}
}
Y ahora la clase que crea las geometrías simples:
//MyGeometricShapeFactory class for creating tessellations.
//Copyright (C) 2012 Benito M. Zaragozi
//Authors: Benito M. Zaragozi (www.gisandchips.org)
//Send comments and suggestions to benito.zaragozi@ua.es
//This program is free software: you can redistribute it and/or modify
//it under the terms of the GNU General Public License as published by
//the Free Software Foundation, either version 3 of the License, or
//(at your option) any later version.
//
//This program is distributed in the hope that it will be useful,
//but WITHOUT ANY WARRANTY; without even the implied warranty of
//MERCHANTABILITY or FITNESS FOR A PARTICULAR PURPOSE. See the
//GNU General Public License for more details.
//
//You should have received a copy of the GNU General Public License
//along with this program. If not, see <http://www.gnu.org/licenses/>.
using System;
using NetTopologySuite.Utilities;
using GeoAPI.Geometries;
using NetTopologySuite.Geometries;
namespace RepeatShapes
{
/// <summary>
/// This class inherites from NTS's GeometricShapeFactory.
/// See that rectangles are created using the parent class.
/// </summary>
public class MyGeometricShapeFactory:GeometricShapeFactory
{
public MyGeometricShapeFactory ()
{
}
private readonly Dimensions _dim = new Dimensions();
private int _nPts = 100;
/// <summary>
/// Creates a triangular polygon.
/// </summary>
/// <returns>
/// The triangle.
/// </returns>
public IPolygon CreateTriangle()
{
int i;
int ipt = 0;
int nSide = _nPts / 100;
if (nSide < 1) nSide = 1;
double XsegLen = this.Envelope.Width/nSide;
double YsegLen = this.Envelope.Width/nSide;
Coordinate[] pts = new Coordinate[3 * nSide + 1];
Envelope env = (Envelope)this.Envelope;
for (i = 0; i < nSide; i++)
{
double x = env.MinX + i * XsegLen;
double y = env.MinY;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MaxX;
double y = env.MinY + i * YsegLen;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MaxX - XsegLen/2;
double y = env.MaxY;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
// for (i = 0; i < nSide; i++)
// {
// double x = env.MinX;
// double y = env.MaxY - i * YsegLen;
// pts[ipt++] = (Coordinate)CreateCoord(x, y);
// }
pts[ipt++] = new Coordinate(pts[0]);
ILinearRing ring = GeomFact.CreateLinearRing(pts);
IPolygon poly = GeomFact.CreatePolygon(ring, null);
return poly;
}
/// <summary>
/// Creates an inverted triangle (up-down).
/// </summary>
/// <returns>
/// The inverted triangle.
/// </returns>
public IPolygon CreateInvertedTriangle()
{
int i;
int ipt = 0;
int nSide = _nPts / 100;
if (nSide < 1) nSide = 1;
double XsegLen = this.Envelope.Width/nSide;
double YsegLen = this.Envelope.Width/nSide;
Coordinate[] pts = new Coordinate[3 * nSide + 1];
Envelope env = (Envelope)this.Envelope;
for (i = 0; i < nSide; i++)
{
double x = env.MinX + i * XsegLen;
double y = env.MaxY;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MinX + XsegLen/2;
double y = env.MinY;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MaxX;
double y = env.MaxY + i * YsegLen;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
pts[ipt++] = new Coordinate(pts[0]);
ILinearRing ring = GeomFact.CreateLinearRing(pts);
IPolygon poly = GeomFact.CreatePolygon(ring, null);
return poly;
}
/// <summary>
/// Creates an hexagon adjusted by a radius parameter.
/// </summary>
/// <returns>
/// The hexagon.
/// </returns>
/// <param name='radius'>
/// A proportion that defines the longitude of the hexagon's base.
/// A larger radius is relate with a narrower base of the hexagon.
/// </param>
public IPolygon CreateHexagon(int radius)
{
int i;
int ipt = 0;
int nSide = _nPts / 100;
if (nSide < 1) nSide = 1;
double XsegLen = this.Envelope.Width/nSide;
double YsegLen = this.Envelope.Height/nSide;
Coordinate[] pts = new Coordinate[6 * nSide + 1];
Envelope env = (Envelope)this.Envelope;
for (i = 0; i < nSide; i++)
{
double x = env.MinX + radius + i * XsegLen;
double y = env.MinY;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MaxX - radius;
double y = env.MinY + i * YsegLen;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MaxX;
double y = env.MinY+(env.Height/2) + i * YsegLen;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MaxX - radius;
double y = env.MaxY + i * YsegLen;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MinX + radius + i * XsegLen;
double y = env.MaxY;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
for (i = 0; i < nSide; i++)
{
double x = env.MinX;
double y = env.MinY+(env.Height/2) + i * YsegLen;
pts[ipt++] = (Coordinate)CreateCoord(x, y);
}
pts[ipt++] = new Coordinate(pts[0]);
ILinearRing ring = GeomFact.CreateLinearRing(pts);
IPolygon poly = GeomFact.CreatePolygon(ring, null);
return poly;
}
}
}
